
|
Calculator Library |

|
|||
| Home » 87 Calculators » Blog » 20 Cool Calculator Functions | |||||
20 COOL CALCULATOR FUNCTIONS
Click here to try our many free online calculators. Alternatively, they can still help you work out the required result if you have the right formula. Check your calculator's manual or online documentation to see the available functions and how to use them. In this article, we'll explore 20 cool things you can do with a calculator that go beyond simple arithmetic. 1. Calculate square roots and cube rootsIf you need to calculate the square root of a number on a calculator, you can use the square root function. This function is usually represented by the symbol √ or is labeled as "sqrt" on the calculator. To find the square root of a number, simply enter the number into the calculator and then press the √ button. For example, to find the square root of 25, you would enter 25 and then press the √ button to get the result of 5. You can use the cube root function to calculate the cube root of a number on a calculator. This function is usually represented by the symbol ∛ or is labeled as "cbrt" on the calculator. To find the cube root of a number, enter the number into the calculator and then press the ∛ button. For example, to find the cube root of 27, you would enter 27 and then press the ∛ button to get the result of 3. If your calculator doesn't have a square root or cube root function, you can still find these roots by raising the number to the appropriate power. To find the square root of a number, you can raise it to the power of 0.5. To find the cube root of a number, you can raise it to the power of 1/3. For example, to find the square root of 25 using this method, you would enter 25 and then press the exponent button (usually represented by the symbol ^ or labeled "pow") and enter 0.5. This would give you the same result as using the square root function. 2. Perform scientific calculations
In addition to basic arithmetic operations, scientific calculators typically have functions for calculating roots, powers and inverse trigonometric functions. They may also have features such as memory and the ability to store and recall calculations, making it easy for users to perform multiple calculations in a row without having to re-enter data. Many scientific calculators also have a built-in display screen that allows users to see their calculations as they are entered, making it easier to check for errors and verify results. While scientific calculators can be valuable tools for performing complex calculations, it's essential for users to be familiar with the functions of their calculators and to use them correctly. Incorrect use of calculator functions can result in inaccurate results, which can be problematic in fields where precision is important. It's also essential for users to be aware of the limitations of their calculators and to use other resources, such as textbooks or online resources, to verify their calculations when necessary. 3. Convert between different units of measurementUsing a calculator to convert between different units of measurement can be very useful in many situations. For example, if you're a cook trying to follow a recipe that calls for ingredients in grams but only have a scale that measures in ounces, you can use a calculator to quickly and easily make the conversion. Another situation where this can be useful is if you're a student working on a math problem that requires you to convert between different units of measurement, such as inches to centimeters or feet to meters. To use a calculator to convert between different units of measurement, you'll first need to find a calculator that has a unit conversion function. For example, you can find our free online Unit Conversion Calculator here. This is typically a feature built into most scientific calculators, but you may also be able to find it on some basic calculators. Once you've found a calculator with this function, you can simply enter the value you want to convert, select the unit of measurement you're starting with, and then select the unit of measurement you want to convert to. The calculator will then perform the conversion for you, giving you the result in the desired unit of measurement. In addition to standard units of measurement such as weight, volume and temperature, some calculators also support more specialized units such as flow rate, density and force. You may need to use a calculator with advanced scientific functions or a unit conversion website to convert between these units. These tools typically allow you to choose from a wide range of unit categories, including engineering, physics and chemistry. 4. Calculate the payments and interest on a loanCalculators that can calculate the payments and interest on a loan typically have a function specifically designed for this purpose. To use this function, you will need to enter the following information: the loan amount, the interest rate and the loan term in months. The calculator will then use this information to determine the monthly payment amount required to repay the loan within the specified time. In addition to calculating the monthly payment, these calculators can also be used to determine the total amount of interest that will be paid throughout the loan. This is useful for comparing loans with different interest rates and terms, as it can help you determine which loan will ultimately cost you the most in interest. Another valuable function of these calculators is the ability to determine the remaining loan balance at any point in time. By entering the current date and number of payments already made, the calculator can determine the remaining balance and time left on the loan. This can be especially helpful for keeping track of your progress in paying off the loan and ensuring you're on track to pay it off on time. 5. Determine the tip at a restaurantCalculator functions can be helpful when determining the tip at a restaurant. Many calculators have a dedicated "tip" function that allows you to quickly calculate the amount you should tip based on the total cost of your meal. To use this function, you'll need to enter the total cost of your meal and the desired tip percentage. The calculator then calculates the dollar amount of the tip and adds it to the total cost of the meal to determine the grand total. Another function that may be included on a calculator is the ability to split the bill between multiple people. For example, if a group of four people are dining at a restaurant and want to split the bill equally, the user can enter the total cost of the meal and the number of people in the group. The calculator will then divide the total cost by the number of people to determine the cost per person, including the tip. Some calculators may also include a feature that suggests a standard tip amount based on the total cost of the meal. This can be helpful for users who are unsure how much to tip or unfamiliar with the tipping customs in the area. The calculator may suggest a range of tip percentages or provide a fixed dollar amount for the tip. 6. Calculate your BMIA BMI calculator is a tool that helps you work out your body mass index (BMI). For example, you can find our free online BMI Calculator here. You'll need to enter your weight and height to use a BMI calculator. The calculator will then use a formula to calculate your BMI. This formula is weight (in kilograms) divided by height (in meters) squared. BMI is a measure of body fat based on height and weight that applies to adult men and women. It's an essential tool for determining if an individual is at a healthy weight. A healthy BMI is generally considered to be between 18.5 and 24.9. A BMI below 18.5 is considered underweight, while a BMI above 24.9 is considered overweight. BMI calculators can be found online or as part of a mobile app. Some calculators also allow you to enter additional information, such as your age and gender, to provide a more accurate reading. It's important to note that BMI isn't a diagnostic tool and should not be used as the sole method for determining if an individual is at a healthy weight. Other factors, such as muscle mass and overall health, should also be considered. 7. Find the area of a shapeThe first step to finding the area of a shape using a calculator is to enter the shape's dimensions into the calculator. This may require using the calculator's basic arithmetic functions to calculate the necessary dimensions if they are not already known. Once all the required dimensions have been entered, the calculator will use a specific formula to calculate the area of the shape. The formula used will depend on the type of shape being measured. For example, the formula for the area of a rectangle is length x width, while the formula for the area of a circle is pi x radius^2. It's important to use the correct formula for the specific measured shape to get an accurate result. In some cases, it may be necessary to use the calculator's trigonometric functions to calculate the dimensions for specific shapes. For example, to find the area of a triangle, you may need to use the calculator's sine function to calculate the length of one of the sides. In other cases, you may need to use the calculator's square root function to find the radius of a circle. Regardless of the specific functions required, the calculator can be a valuable tool for quickly and accurately finding the area of a wide range of shapes. It's also worth noting that some calculators have specific functions for finding the area of certain shapes. For example, many calculators have a dedicated function for finding the area of a circle, which can be accessed by pressing a specific button or entering a specific command. Using these dedicated functions can often be faster and easier than manually entering the relevant dimensions and formula. Regardless of which method is used, the calculator can be a helpful tool for finding the area of a shape quickly and accurately. 8. Calculate the volume of an object
Another way to calculate the volume of an object is to use a calculator's built-in volume function. Many scientific and graphing calculators have a function that can calculate the volume of various shapes such as cylinders, cones and pyramids. To use this function, you would typically enter the relevant dimensions of the shape for which you're trying to calculate the volume. For example, to calculate the volume of a cylinder, you would enter the radius and height of the cylinder. In addition to these methods, some calculators have tools or features specifically designed to help you calculate the volume of irregularly shaped objects. For example, some calculators have a water displacement function that allows you to measure the volume of an object by filling a container with water and measuring the volume of the water displaced by the object. This can be a useful method for calculating the volume of objects with complex shapes that are difficult to measure using other methods. 9. Calculate the distance between two pointsTo calculate the distance between two points using a calculator, you'll need the coordinates of both points. These coordinates can be in the form of (x,y) for two-dimensional space or (x,y,z) for three-dimensional space. Some calculators have a built-in function to calculate the distance between two points. To use this function, you'll need to enter the coordinates of both points into the calculator. The calculator will then use the distance formula, which is distance = √((x2 - x1)^2 + (y2 - y1)^2 + (z2 - z1)^2). The calculator will return the distance between the two points once the calculation is complete. If your calculator doesn't have a built-in distance formula function, you can still use it to calculate the distance manually by entering the distance formula and coordinates of the two points. Alternatively, you can also use online tools or mobile apps to calculate the distance between two points. 10. Convert between polar and rectangular coordinatesA calculator will typically have a function called "polar to rectangular" or "rect" to convert from polar to rectangular coordinates. To use this function, you'll need to enter the polar coordinates, which consist of the magnitude and the angle in radians, separated by a comma. The calculator will then return the rectangular coordinates, which consist of the x and y values. To convert from rectangular to polar coordinates, the calculator will have a function called "rectangular to polar" or "polar". To use this function, you'll need to enter the rectangular coordinates, which consist of the x and y values, separated by a comma. The calculator will then return the polar coordinates, which consist of the magnitude and the angle in radians. It's important to note that some calculators will require you to enter the angle in degrees rather than radians for these conversion functions. In this case, you'll need to use the calculator's degree-to-radian conversion function, typically called "deg" or "degrees", to convert the angle to radians before using the polar-rectangular conversion function. 11. Calculate compound interestMany calculators have a built-in compound interest function. To calculate compound interest for a number of compounding periods using this function, enter the principal amount, the annual interest rate as a decimal (for example, for 5% interest, enter 0.05), the number of compounding periods per year and the total number of compounding periods. For example, you can find our free online Compound Interest Calculator here The calculator will then use the compound interest formula to calculate the total amount of interest earned over the specified number of compounding periods. The formula is A = P(1 + r/n)^(nt), where A is the total amount, P is the principal amount, r is the annual interest rate, n is the number of compounding periods per year and t is the total number of compounding periods. 12. Calculate the fuel efficiency of a carTo calculate the fuel efficiency of a car, you need to know the distance traveled and the amount of fuel consumed over that distance. The fuel efficiency can be calculated using either imperial or metric units. If you're using imperial units, you'll calculate fuel efficiency in miles per gallon (MPG). First, enter the distance traveled in miles on your calculator. Then, enter the amount of fuel consumed in gallons. Finally, divide the distance traveled by the amount of fuel consumed to get the fuel efficiency in MPG. For example, if you traveled 100 miles and used 5 gallons of fuel, your fuel efficiency would be 100/5 = 20 MPG. Alternatively, if you're using metric units, you'll calculate in litres per 100km. In this case, enter the distance traveled in kilometers and the amount of fuel consumed in litres. Finally, divide the amount of fuel consumed by the distance traveled and multiply the result by 100 to get the fuel efficiency in litres per 100km. For example, if you traveled 100km and used 5 litres of fuel, your fuel efficiency would be (5/100)*100 = 5 litres per 100km. It's important to note that the fuel efficiency of a car can vary depending on many factors, including the type of fuel used, the driving conditions and the weight of the vehicle. Therefore, performing these calculations multiple times to get an average fuel efficiency is a good idea. This will give you a more accurate representation of your car's fuel efficiency. 13. Calculate the angle of an inclineTo calculate the angle of an incline using a calculator, you'll first need to determine the incline's rise and run. The rise is the vertical distance between the base of the incline and the top, while the run is the horizontal distance between those two points. Once you've measured the rise and the run, you can use a calculator to determine the angle of the incline. You'll need to use the inverse tangent function, which is usually abbreviated as "tan^-1" or "atan." The inverse tangent function takes the ratio of the rise to the run as its input and returns the angle of the incline in degrees. For example, if the rise is 6 inches and the run is 8 inches, you would enter "atan(6/8)" into the calculator to get the angle of the incline. The result should be approximately 36.87 degrees. You can then use this angle to calculate other properties of the incline, such as its slope or length. 14. Convert between binary and decimal numbers
Converting a decimal number to binary using a calculator is similar. First, press the "Decimal" or DEC button to indicate that the number is in decimal format. Then, enter the decimal number using the numeric keypad. Finally, press the = button to convert the number to binary. The calculator will display the binary equivalent of the decimal number. It's important to note that not all calculators can convert between binary and decimal numbers. If your calculator doesn't have this feature, you can use an online calculator or a scientific calculator to perform the conversion. If you have trouble finding a suitable calculator, you can do these conversions using the calculator built into Windows. 15. Find the slope of a lineTo find the slope of a line using a calculator, you'll need to first enter the coordinates of two points on the line. The slope of the line is equal to the change in the y-coordinate divided by the change in the x-coordinate of the two points. To enter the coordinates of the two points into a calculator, you can use the "x,y" notation, where "x" represents the x-coordinate and "y" represents the y-coordinate. For example, to enter the coordinates (4,5) and (6,7) into a calculator, you would type "4,5 6,7" and then press the slope button. Some calculators may have a dedicated "slope" button, while others may require you to use the "rise over run" formula, which is written as m = (y2 - y1)/(x2 - x1). To use this formula on a calculator, you would enter the coordinates of the two points and then perform the calculation by pressing the necessary buttons in the correct order. 16. Calculate the standard deviation of a set of dataTo calculate the standard deviation of a set of data on a calculator, first enter the data into the calculator as a list. Many calculators have a specific button for this, usually labeled as "Data" or "List." Some calculators may require you to enter the data as a sequence of individual numbers separated by commas or spaces. Once the data has been entered, locate the standard deviation function on the calculator. This is often labeled as "sigma" or "SD," and may be found on a dedicated statistical or mathematics menu. Some calculators may also have a second function for calculating the standard deviation of a sample, labeled as "sigma-n" or "SDS." To use the standard deviation function, select it and then enter the data list as an argument. This is typically done by pressing the button for the data list after choosing the standard deviation function. The calculator will then return the standard deviation of the data as a result. Some calculators may also provide additional statistical information, such as the mean or median of the data. 17. Convert between fractions and decimalsTo convert a fraction to a decimal using a calculator, divide the numerator (top number) by the denominator (bottom number). For example, to convert the fraction 3/4 to a decimal, you would enter 3 divided by 4 into the calculator, giving you 0.75 as the result. If you want to convert a decimal to a fraction using a calculator, you can use the "fraction" button or key, which is often labeled with a symbol that looks like a fraction. For example, to convert the decimal 0.75 to a fraction, you would enter 0.75 and then press the fraction button. The calculator will then display the fraction 3/4 as the result. It's important to note that some calculators may not have a fraction button, in which case you can use the "decimal to fraction" or "fraction to decimal" conversion functions, which are often found under the "math" or "conversion" menus on the calculator. You may also be able to find online calculators or smartphone apps that can help you convert fractions to decimals and vice versa. 18. Calculate the surface area and volume of a sphereTo calculate the surface area and volume of a sphere using a calculator, you'll need to know the radius of that sphere. The radius is the distance from the center of the sphere to any point on its surface. The surface area of a sphere is equal to 4 times pi times the radius squared, so the formula is 4πr2. If the radius is 10 inches, you can calculate the answer by entering 4 x 𝜋 x 10 x2 = giving a result of 1256.64 in2, rounded to 2 decimal places. The volume of a sphere is equal to 4⁄3 times pi times the radius cubed, so the formula is 4⁄3πr3. Again, if the radius is 10 inches, you can calculate the answer by entering 4 ÷ 3 x 𝜋 x 10 xy 3 = giving a result of 4188.79 in3, rounded to 2 decimal places. Alternatively, some calculators may have a dedicated function for calculating the surface area or volume of spheres, so you may be able to use this function to calculate these values more quickly. 19. Calculate the distance, speed and time of a journeyIf you want to work out the distance of a journey using a calculator, you'll need to enter the speed and time of the journey into the formula distance = speed x time. For example, if you were driving at a speed of 60 miles per hour for 3 hours, the distance you traveled would be 60 x 3 = 180 miles. To find the speed of a journey, use the formula speed = distance / time with the distance traveled and time it took to complete the journey. For instance, if you traveled a distance of 200 miles in 4 hours, your speed would be 200 / 4 = 50 miles per hour. To calculate the time it took to complete a journey, enter the distance traveled and the speed into the formula time = distance / speed. For example, if you traveled a distance of 300 miles at a speed of 60 miles per hour, it would take you 300 / 60 = 5 hours to complete the journey. 20. Determine the probability of an event occurring
Another way to use a calculator to determine probability is by entering the total number of possible outcomes and the number of favorable outcomes. For example, if you're drawing a card from a deck of 52 and want to know the probability of drawing a heart, you can enter "13" as the number of favorable outcomes (since there are 13 hearts in a deck) and "52" as the total number of possible outcomes. The calculator will then output the probability of drawing a heart, which is 13/52 or approximately 0.25. Finally, many calculators also have a built-in probability function that allows you to enter the number of successes, the number of trials and the probability of success for each trial. For example, suppose you're flipping a coin and want to know the probability of getting 3 heads in a row. In that case, you can enter "3" as the number of successes, "3" as the number of trials and "0.5" as the probability of success (since the probability of getting heads on a coin flip is 1/2 or 0.5). The calculator will then output the probability of getting 3 heads in a row, which is approximately 0.125. ConclusionAs you can see, you can do many surprising things with a calculator beyond just basic math operations. Whether you're working with complex scientific calculations, converting between units of measurement or solving systems of equations, a calculator can be a valuable tool. So next time you reach for your calculator, remember that it's capable of much more than just adding and subtracting.
|
|
||||
Copyright © Calculator Library, 1998 - 2025. Made with ♥ in Australia. |
|||||
 Calculators are often thought of as simple devices used for basic operations like addition, subtraction, multiplication and division. However, most are
capable of much more than just simple arithmetic. Often there are cool functions built into the calculator to help you calculate the things you need quickly and
easily.
Calculators are often thought of as simple devices used for basic operations like addition, subtraction, multiplication and division. However, most are
capable of much more than just simple arithmetic. Often there are cool functions built into the calculator to help you calculate the things you need quickly and
easily. Scientific calculators are specialized calculators that are designed to perform advanced mathematical and scientific calculations. Many scientific calculators
have a range of functions that allow users to perform complex calculations and operations, such as trigonometry, logarithms and exponentiation. Some scientific
calculators even have specialized functions for fields such as engineering and statistics, making them essential tools for students and professionals in these
fields.
Scientific calculators are specialized calculators that are designed to perform advanced mathematical and scientific calculations. Many scientific calculators
have a range of functions that allow users to perform complex calculations and operations, such as trigonometry, logarithms and exponentiation. Some scientific
calculators even have specialized functions for fields such as engineering and statistics, making them essential tools for students and professionals in these
fields.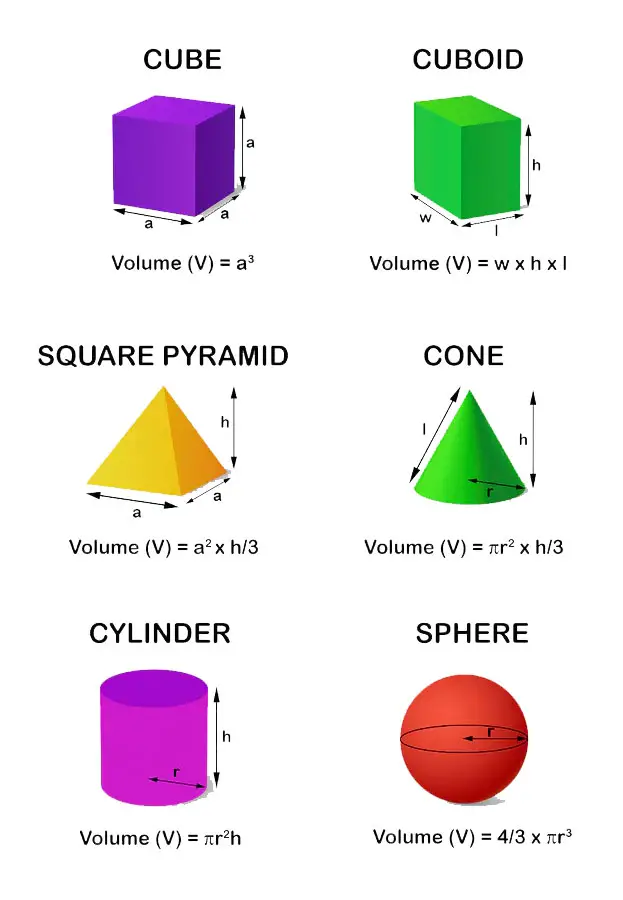 There are several ways to calculate the volume of an object using a calculator. One standard method is to use the formula for the volume of a shape. For
example, to calculate the volume of a cube, you would use the formula
There are several ways to calculate the volume of an object using a calculator. One standard method is to use the formula for the volume of a shape. For
example, to calculate the volume of a cube, you would use the formula  On some calculators, you may need to select "Programmer" mode before performing this calculation. Then, if you want to convert a binary number to decimal,
press the "Binary" or BIN button to indicate that the number is in binary format. Next, enter the number using the numeric keypad. Finally, press
the = button to convert the number to decimal. The calculator will display the decimal equivalent of the binary number.
On some calculators, you may need to select "Programmer" mode before performing this calculation. Then, if you want to convert a binary number to decimal,
press the "Binary" or BIN button to indicate that the number is in binary format. Next, enter the number using the numeric keypad. Finally, press
the = button to convert the number to decimal. The calculator will display the decimal equivalent of the binary number. Calculators can be used to determine the probability of an event occurring in a few different ways, depending on the information available. One way to do this
is to use the binomial probability formula, which calculates the probability of a specific number of successes occurring in a certain number of trials. For
example, if you're rolling a die and want to know the probability of rolling a 3, you can enter "1" as the number of successes and "6" as the number of trials.
The calculator will then output the probability of rolling a 3, which is 1/6 or approximately 0.17.
Calculators can be used to determine the probability of an event occurring in a few different ways, depending on the information available. One way to do this
is to use the binomial probability formula, which calculates the probability of a specific number of successes occurring in a certain number of trials. For
example, if you're rolling a die and want to know the probability of rolling a 3, you can enter "1" as the number of successes and "6" as the number of trials.
The calculator will then output the probability of rolling a 3, which is 1/6 or approximately 0.17.