|
Calculator Library |

|
|||
| Home » 87 Calculators » Blog » How To Find Zeros On A Graphing Calculator | |||||
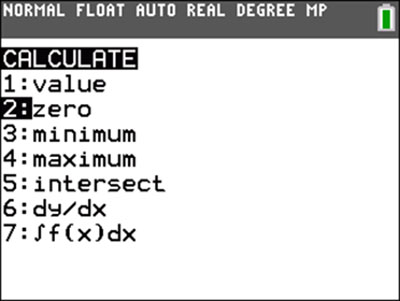
HOW TO FIND ZEROS ON A GRAPHING CALCULATOR
What are Zeros and Why are They Important?Before diving into the details of finding zeros on a graphing calculator, it's essential to understand what zeros are and why they are important. A function's zero, or root, is a value of the input (x) that results in an output (y) of zero. In other words, it's a point at which the function crosses the x-axis. Zeros are essential because they can give us insight into the behavior of a function. For example, if we know that a function has a zero at x=2, it tells us the function will cross the x-axis at that point. Steps For Finding Zeros on a Graphing Calculator
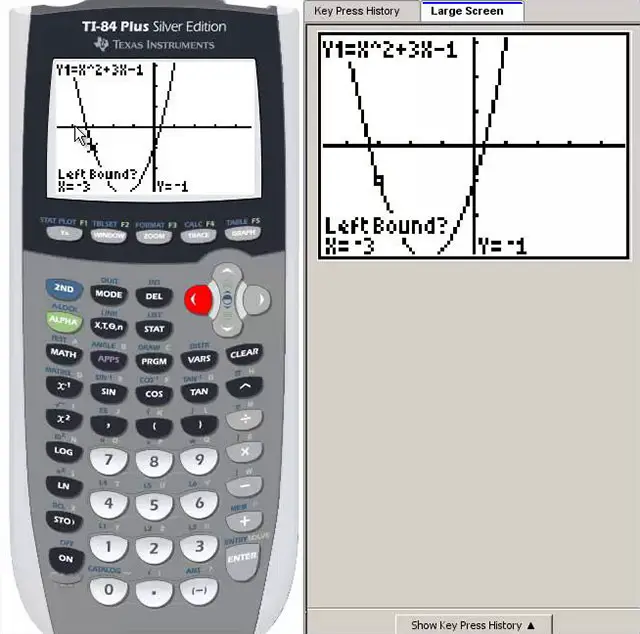
Step 1: Enter the FunctionThe first step in finding zeros on a graphing calculator is to enter the function for which you want to find the roots. This is typically done by pressing the y= button and then typing in the function using the calculator's keypad. For example, to enter the function y = x^2 - 3x + 2, you would press y=, type "x^2-3x+2" and then press the enter button. Step 2: Plot the GraphOnce you've entered the function, the next step is to plot the function's graph. This is typically done by pressing the graph button, which will display the function's graph on the calculator's screen. If the graph isn't displayed correctly, you may need to adjust the viewing window by pressing the window button and entering the desired viewing range for the x- and y-axes. Step 3: Find the ZerosNow that the function's graph is displayed on the screen, the next step is to find the zeros. There are a few different methods for doing this, depending on the type of graphing calculator you're using.
Tips and TricksHere are some tips and tricks for finding zeros on a graphing calculator:
Other Methods To Find Zeros Of A FunctionWhile finding zeros on a graphing calculator is convenient and efficient, it's not the only way to find zeros of a function. Here are a few other ways that you can find zeros of a function:
Other Applications of Finding ZerosIn addition to analyzing the behavior of a function, finding zeros on a graphing calculator has several other applications. For example, you can use zeros to solve equations with no closed-form solution, such as those involving radicals or logarithms. You can also use zeros to find the points of intersection between two functions, which can be helpful in finding the solution to a system of equations. Another application of finding zeros on a graphing calculator is optimization. By finding the zeros of the derivative of a function, you can determine the points at which the function has a local maximum or minimum. This can be useful for finding the optimal solution to a problem, such as finding the minimum cost of a production process or the maximum profit of a business. Troubleshooting Common ProblemsWhile finding zeros on a graphing calculator is generally a straightforward process, there are a few common problems that you may encounter. Here are some troubleshooting tips for dealing with these problems:
Real-World ExamplesNow that we have gone over the steps and techniques for finding zeros on a graphing calculator let's look at a few examples of how this tool can be used in the real world. Example 1: Solving an EquationSuppose we want to find the value of x that satisfies the equation x^3 - 6x^2 + 11x - 6 = 0. We can use a graphing calculator to find the zeros of this equation. To do this, we would enter the equation into the calculator and set the window to a suitable range. Then, we would use the zero feature to find the zeros within the specified range. The calculator would then display the values of x at which the zeros occur. Example 2: OptimizationSuppose we have a function that represents the cost of producing a particular product as a function of the number of units produced. We want to find the value of x that minimizes the cost. To do this, we can use the derivative of the cost function to find the points at which the function has a local minimum. We can then use the zero feature on the derivative to find the zeros, the points at which the derivative is zero. The value of x at these points will be the values that minimize the cost function. Example 3: Intersection of Two FunctionsSuppose we have two functions representing a certain product's supply and demand. We want to find the point at which the two functions intersect, which will represent the equilibrium price. To do this, we can use the intersect feature on the graphing calculator to find the points at which the two functions intersect. The value of x at these points will be the equilibrium price. Frequently Asked QuestionsHere are some frequently asked questions about finding zeros on a graphing calculator: Q: Can I find zeros of non-polynomial functions on a graphing calculator? A: Yes, you can find zeros of non-polynomial functions on a graphing calculator. While the polynomial root finder only applies to polynomial functions, you can use the zero feature to find zeros of any function. Q: Can I find all of the zeros of a function on a graphing calculator? A: It depends on the function. Some functions may have infinite zeros, while others may have a finite number. In general, you can find all of the zeros of a function within a specific range on a graphing calculator. However, you may need to search multiple times using different ranges to find all the zeros. Q: How do I find the x-intercept of a function on a graphing calculator? A: The x-intercept of a function is a zero of the function. To find the x-intercept on a graphing calculator, you can use the zero feature to find the function's zeros. The x-intercept will be the value of x at which the zero occurs. Q: Can I find zeros of a function on a graphing calculator if the function isn't continuous? A: No, you can't find zeros of a function on a graphing calculator if the function isn't continuous. A graphing calculator's zero feature will only find continuous function zeros. If the function is discontinuous, you must find the zeros manually or use another method. ConclusionIn this article, we've seen that finding the zeros of a function using a graphing calculator is a relatively straightforward process that can save you time and effort when solving math and science problems. By following the steps outlined above, you can quickly and easily find a function's roots using various methods, depending on the type of calculator you're using and the complexity of the function. If your function doesn't have any zeros or has an infinite number of zeros, you can still use advanced techniques like the "intersect" function to find the x-coordinates of the points where the curve of the function comes closest to the x-axis. With a little practice, you'll find the zeros of any function with confidence and ease.
|
|
||||
Copyright © Calculator Library, 1998 - 2025. Made with ♥ in Australia. |
|||||
 Graphing calculators are essential tools for many math and science courses, allowing students to quickly and easily plot graphs, solve equations and perform many other mathematical tasks. One particularly valuable feature of these calculators is the ability to find a function's zeros, or roots. In this
article, we'll cover the steps for finding zeros on a graphing calculator and provide some tips and tricks for getting the most out of this feature.
Graphing calculators are essential tools for many math and science courses, allowing students to quickly and easily plot graphs, solve equations and perform many other mathematical tasks. One particularly valuable feature of these calculators is the ability to find a function's zeros, or roots. In this
article, we'll cover the steps for finding zeros on a graphing calculator and provide some tips and tricks for getting the most out of this feature.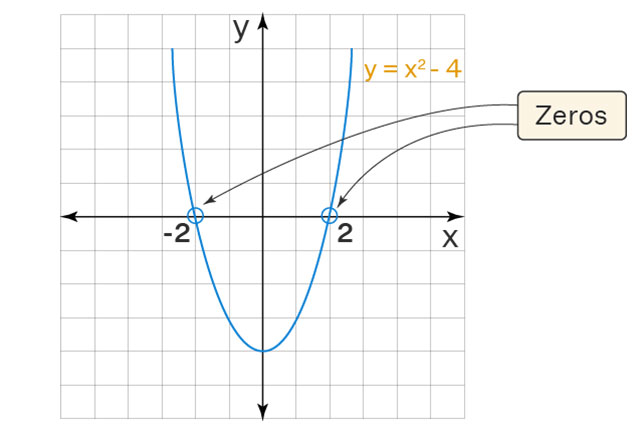 Now that we have a basic understanding of what zeros are and why they are essential, let's go over the steps for finding zeros on a graphing calculator.
Now that we have a basic understanding of what zeros are and why they are essential, let's go over the steps for finding zeros on a graphing calculator.